Tiu unua ekzemplo ebligis vin kompreni la nocion de sistemo de Lindenmayer, eble sen ekkonscii kiel ni uzos tion konkrete kun la testudo.
Ja tie tio estiĝas interesa: Ĉiu vorto tiel konstruita nur havas propran signifon. Oni tiam kroĉos al ĉiu litero de la sinsekvo, komandon rulotan de la testudo, por tiel generi desegnojn 2D aŭ 3D.
Ni prenu por ekzemplo α = 90 kaj unuecan moviĝon je 10 testudpaŝojn; jen:
|
Unuaj iteracioj:




|
Programo en Logo:
por neĝero :p provizu "unuo 300 / potencon 3 :p-1 ripetu 3 [F :p-1 td 120] fino por F :p se :p=0 [an :unuo haltu] F :p-1 mdn 60 F :p-1 dn 120 F :p-1 md 60 F :p-1 fino |
Jen la unuaj reprezentoj uzante α = 90 kaj alĝustigante la unuecan paŝon tiel ke la figuro havu ĉiam la saman amplekson:



|
Tre facilas do krei la programon Logo ebligantan generi tiujn desegnojn:
# p indikas l’ iteracion
por koch :p
# Je ĉiu iteracio, la unueca distanco dividatas per 4
# Ĉi tie, la fina figuro havos amplekson 600x600 maksimume
provizu "unuo 300 / potencon 4 :p-1
ripetu 3 [F :p-1 tg 90] F :p-1
fino
# La ĉeno reskribada
por F :p
se :p=0 [an :unuo haltu]
F :p-1 mdn 90 F :p-1 dn 90 F :p-1 dn 90
F :p-1 F :p-1 mdn 90 F :p-1 mdn 90 F :p-1 dn 90 F :p-1
fino
|
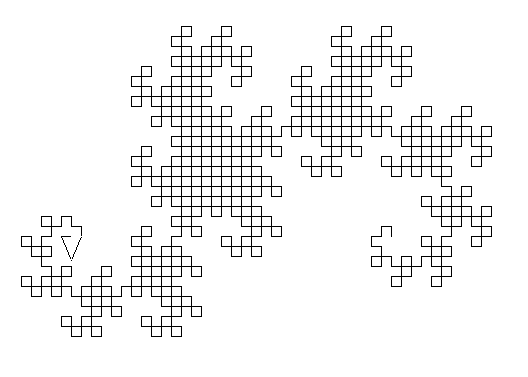
A → A + B+ |
B →−A − B |
por a :p se :p=0 [an :unuo haltu] a :p-1 mdn 90 b :p-1 mdn 90 fino por b :p se :p=0 [an :unuo haltu] dn 90 a :p-1 dn 90 b :p-1 fino por dragono :p provizu "unuo 300 / 8 / :p a :p fino |

|
La sekva ekzemplo estas la kurbo de Hilbert en la spaco; ĝi estas kurbo kun la atributo plenigi tute kubon kiam oni pligrandigas la nombron de iteracioj .
Jen la rilata sistemo:
A → B − F + CFC + F − D&F^D − F + &&CFC + F + B∕∕ |
B → A&F^CFB^F^D^^ − F − D^|F^B|FC^F^A∕∕ |
C →|D^|F^B − F + C^F^A&&FA&F^C + F + B^F^D∕∕ |
D →|CFB − F + B|FA&F^A&&FB − F + B|FC∕∕ |
por hilbert :p
ev perspektive
provizu "unuo 400 / potencon 2 :p
linia_difino sdikp :unuo/2
a :p
linia_difinhalto
tridimensie_vidigu
fino
por a :p
se :p=0 [haltu]
b :p-1 dn 90 an :unuo mdn 90 c :p-1 an :unuo c :p-1
mdn 90 an :unuo dn 90 d :p-1 malsupren 90 an :unuo supren 90 d :p-1
dn 90 an :unuo mdn 90 malsupren 180 c :p-1 an :unuo c :p-1
mdn 90 an :unuo mdn 90 b :p-1 dfn 180
fino
por b :p
se :p=0 [haltu]
a :p-1 malsupren 90 an :unuo supren 90 c :p-1 an :unuo b :p-1 supren 90
an :unuo supren 90 d :p-1 supren 180 dn 90 an :unuo dn 90 d :p-1 supren 90
dn 180 an :unuo supren 90 b :p-1 dn 180 an :unuo c :p-1 supren 90 an :unuo
supren 90 a :p-1 dfn 180
fino
por c :p
se :p=0 [haltu]
dn 180 d :p-1 supren 90 dn 180 an :unuo supren 90 b :p-1 dn 90 an :unuo mdn 90
c :p-1 supren 90 an :unuo supren 90 a :p-1 malsupren 180 an :unuo a :p-1 malsupren 90
an :unuo supren 90 c :p-1 mdn 90 an :unuo mdn 90 b :p-1 supren 90 an :unuo supren 90
d :p-1 dfn 180
fino
por d :p
se :p=0 [haltu]
dn 180 c :p-1 an :unuo b :p-1 dn 90 an :unuo mdn 90 b :p-1 dn 180
an :unuo a :p-1 malsupren 90 an :unuo supren 90 a :p-1 malsupren 180 an :unuo
b :p-1 dn 90 an :unuo mdn 90 b :p-1 dn 180 an :unuo c :p-1 dfn 180
fino
|
Jen l’ unuaj iteracioj:




|